카카오 코드 페스티벌 예선 5번, 캠핑
Contents
안녕하세요. 오늘은 카카오 코드 페스티벌 예선에 나온 5번 캠핑 문제에 대해 풀이를 해보겠습니다.
문제는 https://www.welcomekakao.com/learn/challenges/667 에서 확인하실 수 있습니다.
시간 복잡도
간단히 모든 경우의 수를 다 고려한다고 생각하고 시간 복잡도를 간단히 생각해보면, 1개의 쐐기에 대해 본인 쐐기를 제외한 N-1 개의 쐐기와 쌍을 지어서,
나머지 N-2 쐐기에 대해 주어진 조건을 만족하는지 확인해야 합니다.쐐기가 N 개이니까, N*(N-1)*(N-2), 이므로 O(n^3)이 되기 때문에 풀기가 힘들어집니다.
팁으로 N의 개수와 시간 복잡도를 어림짐작할 때 쓸 수 있는 방법으로, 주먹구구 법칙이라는 게 있는데요.
간단히 말해서, O(x) 일 때 x가 1억을 넘어가면 시간 초과가 나기 쉽다는 말입니다.위의 경우 x = n^3이고, n이 최대 5000이기 때문에 5000개에 대해서 수행할 때는
1250억 정도가 나옵니다. 제한된 시간 내에는 절대 불가능합니다. 적어도 N^2 까지는 줄여줘됩니다.
※자세한 내용은 http://book.algospot.com/estimation.html 를 참고하세요.
해당 문제에서는 S[i][j] 배열을 만들어 (0,0)을 기준으로 x좌표가 i, y좌표가 j인 사각형 내부에(경계선 포함) 존재하는 쐐기의 개수를 미리 구함으로써쐐기 쌍이 선택됐을
때(N*(N-1) 개) 텐트가 만들어질 수 있는 조건을 S를 참고해 바로 구함으로써 N^2의 시간에 수행할 수 있게 됩니다.
(x, y) , (x2, y2) 쌍의 사각형 내부에 쐐기가 있는지 없는지를 확인하려면
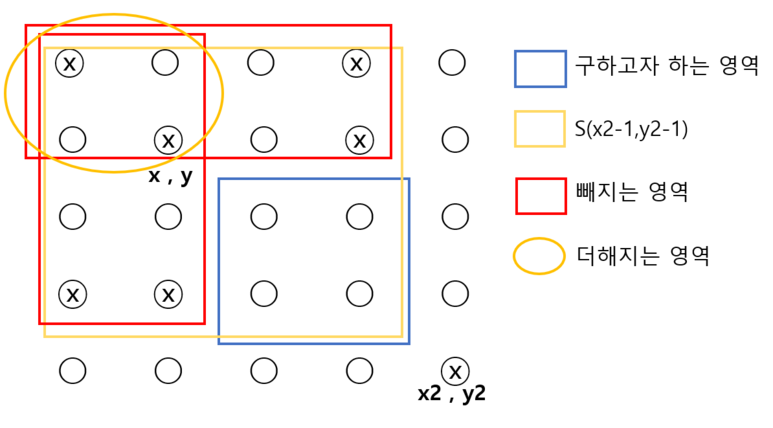
그림에서 파란색 박스가 구하고자 하는 영역입니다. 이 영역을 구하기 위해서는, S[x2-1][y2-1] 의 영역에서 빨간색으로 된 부분을빼줘야 됩니다.
다만 겹치는 부분이 있기 때문에 이 부분은 다시 + 해줘야 됩니다!
식으로 정리하자면(x, y) (x2, y2) 내부 쐐기 = S[x2-1][y2-1] - S[x2-1][y] - S[x][y2-1] + S[x][y]가 됩니다. 몇 번의 덧셈 연산으로 내부의 쐐기가 있는지 없는지 확인 가능하게
됩니다. 추가적으로 필요한 개념이 좌표 압축인데요. 추가할 예정입니다. 우선은 구글링으로..다음 포스팅에서는 해당 문제를 최적화를 통해
N^3으로 푼 경우와(코드가 되게 깔끔하더라고요)좌표 압축에 대해서 올리겠습니다!
————————————————————–풀이 코드————————————————
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 |
#include <vector>
#include <cstring>
#include <cstdio>
#include <algorithm>
#include <unordered_set>
using namespace std;
// 전역 변수를 정의할 경우 함수 내에 초기화 코드를 꼭 작성해주세요.
int S[5000][5000]; //내부 쐐기의 개수 저장 배열
int solution(int n, vector<vector<int>> data) {
memset(S, 0, sizeof S); // 0으로 세팅
vector<int> xpoints; // x좌표 집합
vector<int> ypoints; // y좌표 집합
for (int i = 0; i < data.size(); i++) { //데이터에 있는 좌표를 x,y로 나누어 넣음
xpoints.push_back(data[i][0]);
ypoints.push_back(data[i][1]);
}
unordered_set<int> uniqXpoints(xpoints.begin(), xpoints.end()); // 중복 값 제거를 위해 셋에 넣음
unordered_set<int> uniqYpoints(ypoints.begin(), ypoints.end());
xpoints.clear(); //중복제거된 값을 다시 넣기 전에 clear
ypoints.clear();
xpoints.assign(uniqXpoints.begin(), uniqXpoints.end()); //중복제거된 값을 다시 넣기
ypoints.assign(uniqYpoints.begin(), uniqYpoints.end());
sort(xpoints.begin(), xpoints.end()); // 정렬
sort(ypoints.begin(), ypoints.end());
int x = 0, y = 0; //좌표 압축
for (int i = 0; i < data.size(); i++) {
for (int j = 0; j < xpoints.size(); j++) {
if (data[i][0] == xpoints[j]) {
x = j;
data[i][0] = x; // 좌표를 인덱스로 교체
break;
}
}
for (int k = 0; k < ypoints.size(); k++) {
if (data[i][1] == ypoints[k]) {
y = k;
data[i][1] = y; // 좌표를 인덱스로 교체
break;
}
}
S[x][y] = 1; // 쐐기가 있는 곳은 미리 1로 설정
}
// 각 영역별 쐐기 값을 누적으로 누하기
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
S[i][j] += (i - 1 > -1 ? S[i - 1][j] : 0) + (j - 1 > -1 ? S[i][j - 1] : 0) - (i - 1 > -1 && j - 1 >-10 ? S[i - 1][j - 1] : 0);
}
}
int ans = 0;
int cnt = 0;
int startX, startY, endX, endY;
// 모든 쐐기에 대해 조사
for (int i = 0; i < n; i++) {
for (int j = i + 1; j < n; j++) {
// 크기 1이상의 직사각형이 아닌경우
if (data[i][0] == data[j][0] || data[i][1] == data[j][1]) continue;
// 크기 1이상의 직사각형이 존재하는 경우
cnt = 0;
startX = data[i][0] < data[j][0] ? data[i][0] : data[j][0];
startY = data[i][1] < data[j][1] ? data[i][1] : data[j][1];
endX = data[i][0] > data[j][0] ? data[i][0] : data[j][0];
endY = data[i][1] > data[j][1] ? data[i][1] : data[j][1];
//내부의 공간이 1 인 경우, 쐐기가 있을 공간이 없음
if (startX + 1 > endX - 1 || startY + 1 > endY - 1) {
cnt = 0;
}
else {
//
cnt = S[endX - 1][endY - 1] - S[endX - 1][startY] - S[startX][endY - 1] + S[startX][startY];
}
if (cnt == 0) ans++; //내부에 존재하는 쐐기의 개수가 0이면 가능한 경우
}
}
return ans;
} |
Author Jaejin Jang
LastMod 2017-12-23
License Jaejin Jang