1. Binary Classification
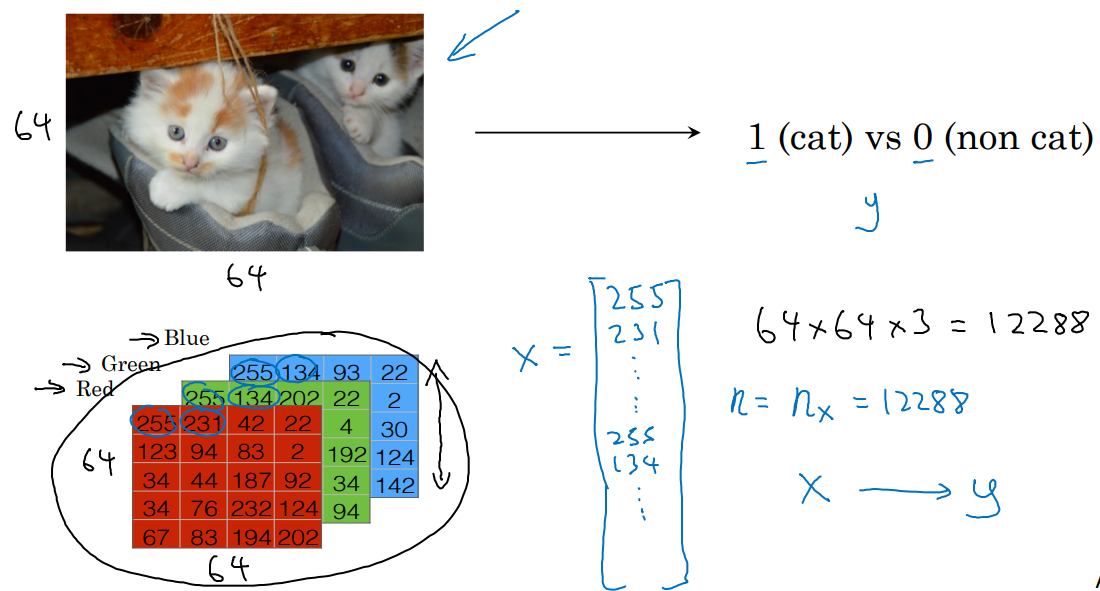
- y가 0, 1일 때 사용하는 분류입니다.
- 로지스틱 회귀(Logistic regression)는 이진 분류를 위한 알고리즘 중 하나입니다.
2. Notation
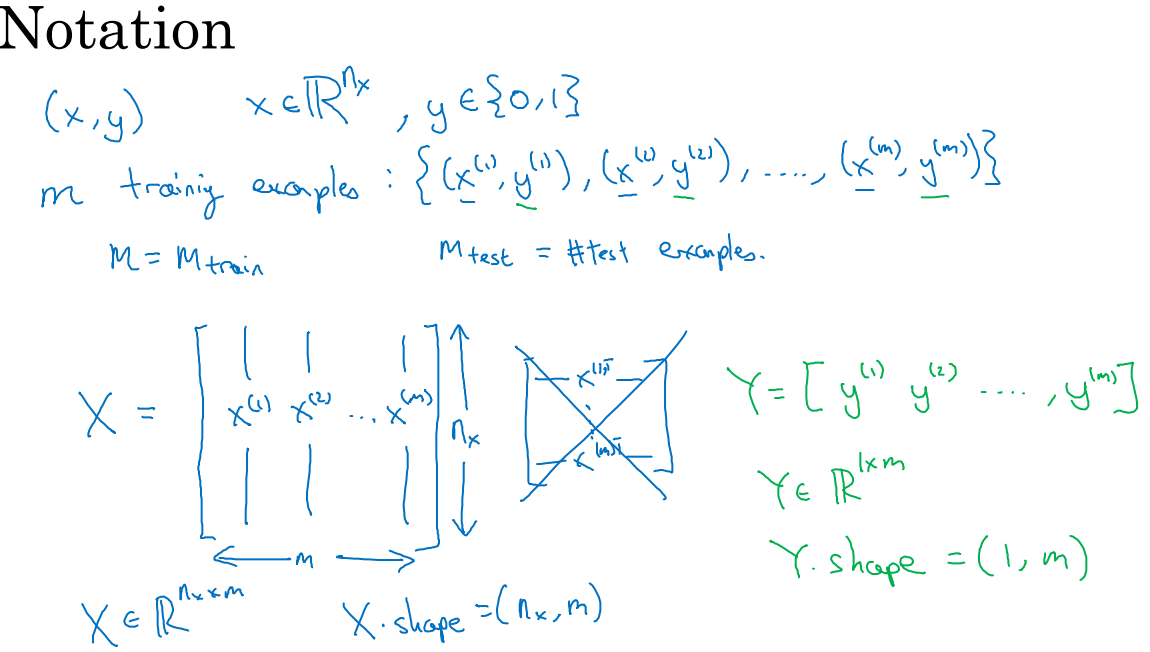
- 수식들을 표기위한 Notation, 너무 중요합니다. 꼭 이해하고 사용할 수 있어야합니다.
- x(i)를 열로 쌓는 방식도 있다고 하는데 사용안한다고 하네요(그림에 보면 엑스로 표시). 행으로 쌓는 방식이 계산에 더 유리하다고 합니다.
3. Logistic Regression
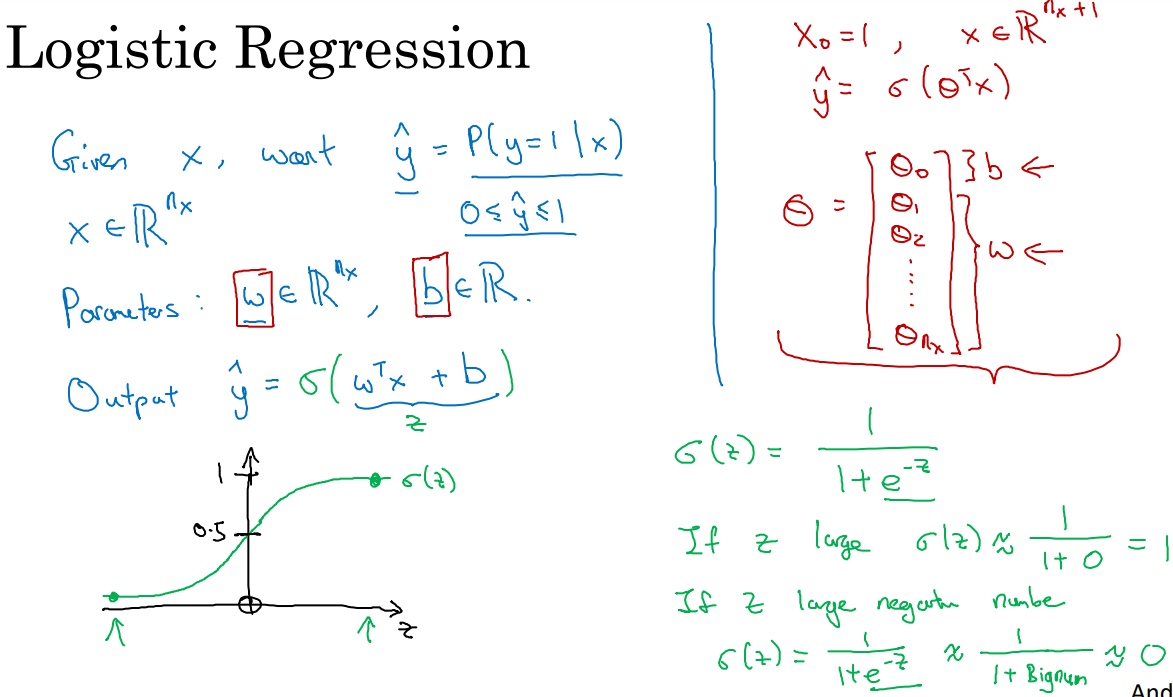
- 로지스틱 회귀 알고리즘을 사용한다면, 딥러닝은 학습을 통해 파라미터 w, b를 구하는 과정입니다.
- 오른쪽에 보시면 쎄타(theta)로 w, b를 한번에 표현하는 방식이 있는데 별로라고합니다. w, b로 나눠서 처리하는 것이 낫다고 하네요. 이유는 잘모르겠습니다. 별개의 변수이니 나눠서 처리하는 것이 이해하기 쉽겠죠?
4. Logistic Regression cost function

- 손실(loss)은 오차를 의미합니다. 손실은 y의 값과 y^의 차이입니다. 딥러닝은 학습을 통해 가장 손실이 낮은 파라미터를 찾아내는 과정이 되겠네요.
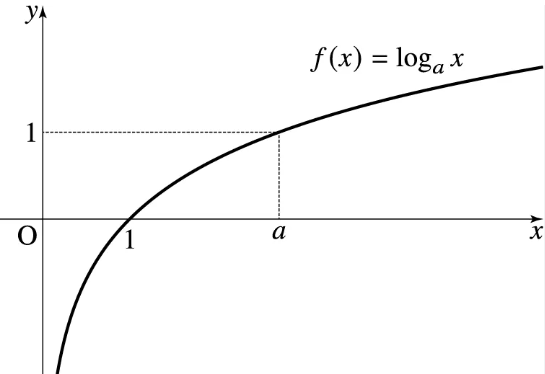
- loss 함수는 정해져있는 건 아닌것 같습니다. 보통 $$ L(\hat{y}, y) = 1/2{(\hat{y} - y)}^2 $$ 을 사용하는 것 같은데 logistic regression에는 로그로 표현한 $$ L(\hat{y}, y) = -(y\log{\hat{y}} + (1-y)\log({1-\hat{y}})) $$ 을 사용합니다.
- 녹색 필기부분을 이해하는 것이 중요합니다. y = 0, 1일때를 나눠서 설명하고 있습니다.
- y = 1 일때, 우리는 y^을 1에 가깝게 만들기를 원하고 그것은 loss가 0에 가깝기를 원하는 것과 같습니다. x가 1일때 0이 되는 로그함수와 정확하게 일치하는 개념입니다.
- y = 0 일때는 반대로 생각하시면 됩니다.
- 비용(cost) 함수는 m개의 훈련세트에 대한 손실을 m으로 나눈것입니다. 손실의 평균을 의미하네요.
5. Gradient Descent
- 기울기 하강(Gradient Descent)라는 개념자체를 알고 시작하는 것이 좋습니다.

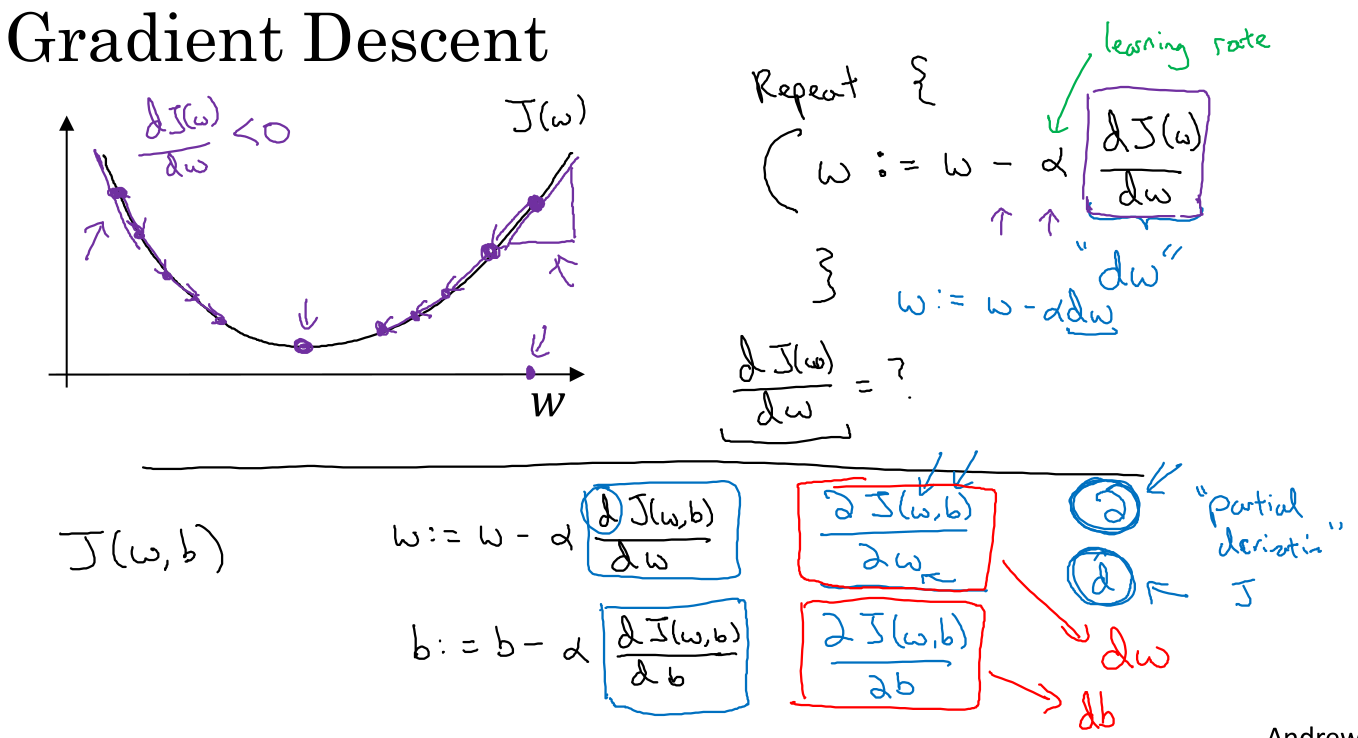
- 기하학적으로 볼때 훈련을 반복하면서 볼록한 지점(비용이 최소)인 지점으로 점점 하강하는 과정을 상상할 수 있습니다.
- 볼록한 형태라는 것은 이미 밝혀져 있는 사실이라고 하네요. 이것이 궁금하면 수학과로 ㄱㄱ
6. Derivatives
- 이건 알아서 공부하시길..
7. More derivatives examples
- 이건 알아서 공부하시길..
8. Computation Graph
- Computation graph는 mathematical expression을 directed (acyclic) graph로 표현한 것입니다. 각 node는 하나의 operation(혹은 function)을 나타냅니다.

- 수식(cost function)이 주어졌을때, 그래프로 표현할 수 있습니다. 굳이 그래프로 표현하는 이유는 쉽게 이해하기 위함이라고 생각합니다. 각 계산과정이 레이어로 표현되어 과정을 한눈에 볼수있으니까요.
9. Derivatives with a Computation Graph
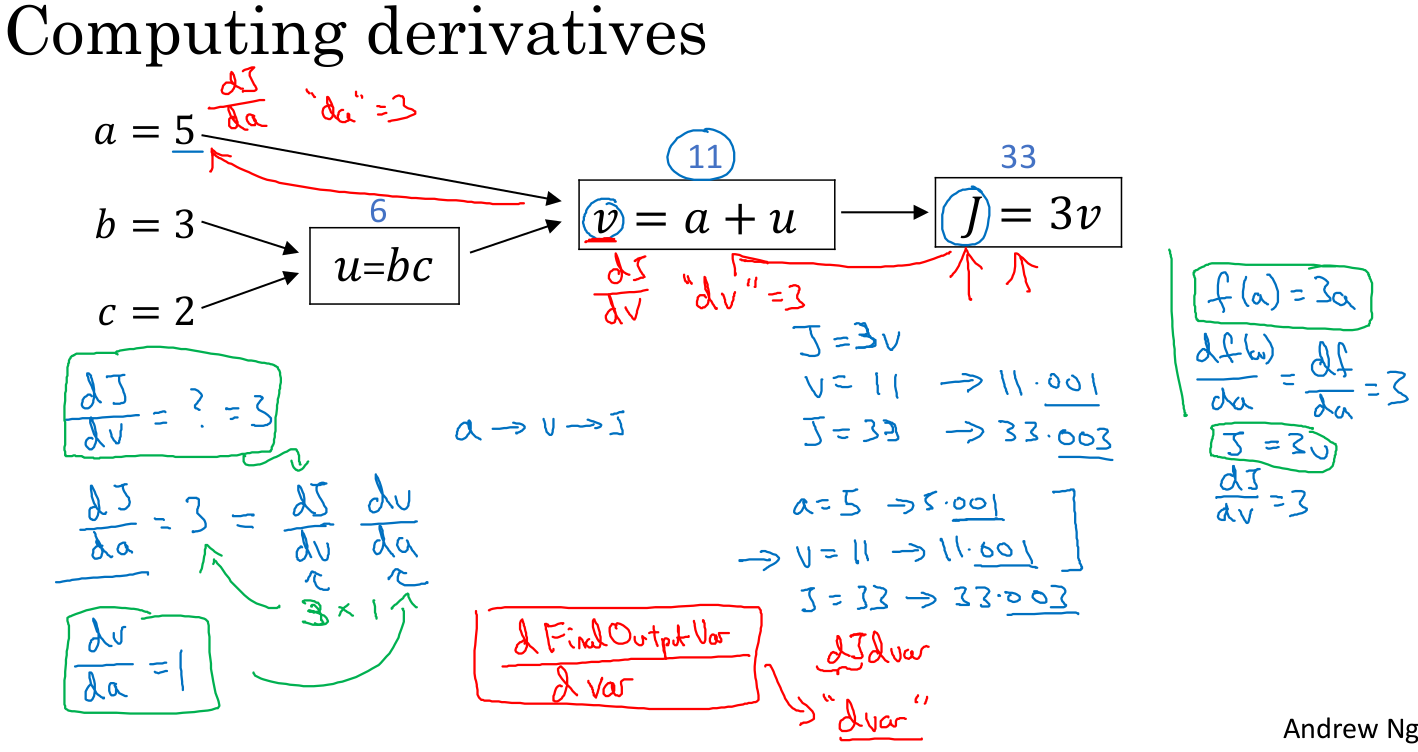

- 계산 그래프에서 앞으로 계산해나가는 것(전파)이 비용을 계산하는 것이라면, 뒤로 계산해 나가는것(역전파)는 각 수식에서 도함수를 구하는 과정입니다.
10. Logistic Regression Gradient descent
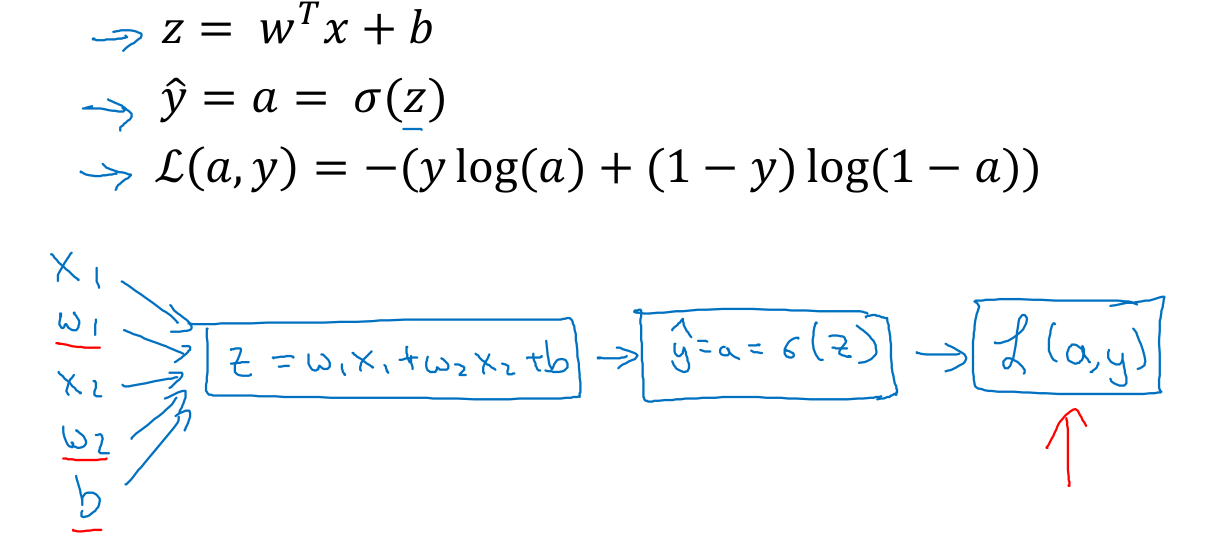
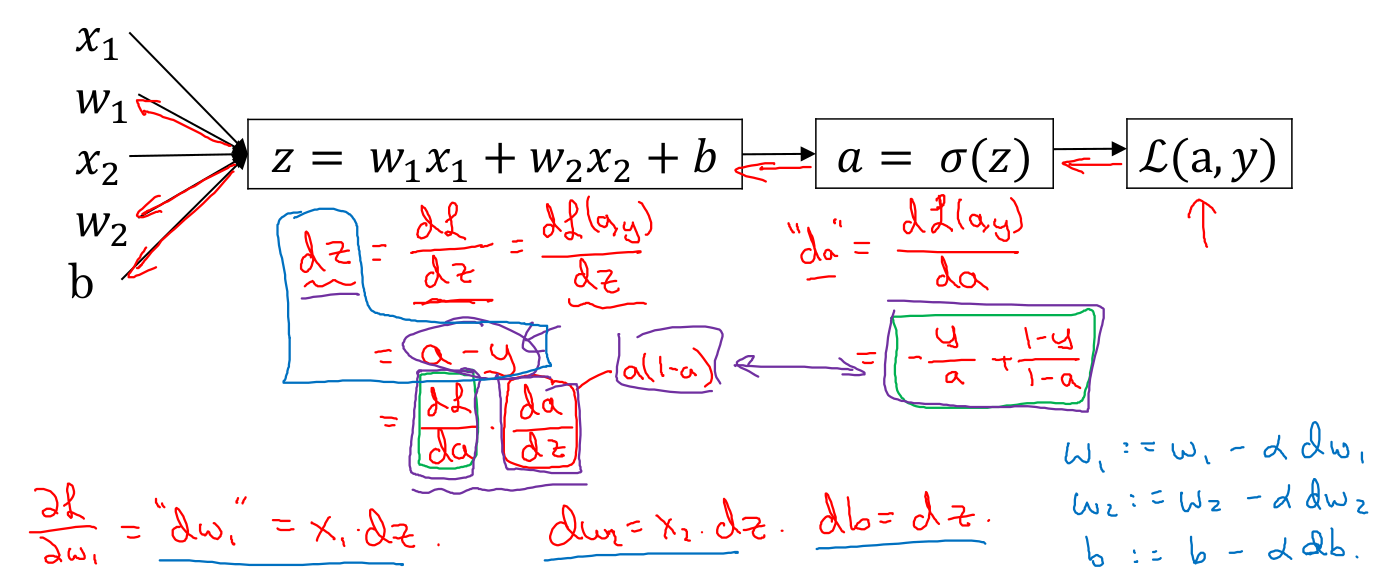
- 빨간선을 오른쪽에서 왼쪽으로 보면 연쇄법칙을 이용해 각 도함수를 구해나가는 과정을 볼 수 있습니다.
- 로그함수의 미분과 시그모이드 함수의 미분을 알아야 합니다. 미분표 참고하면 됩니다.
11. Gradient descent on m examples
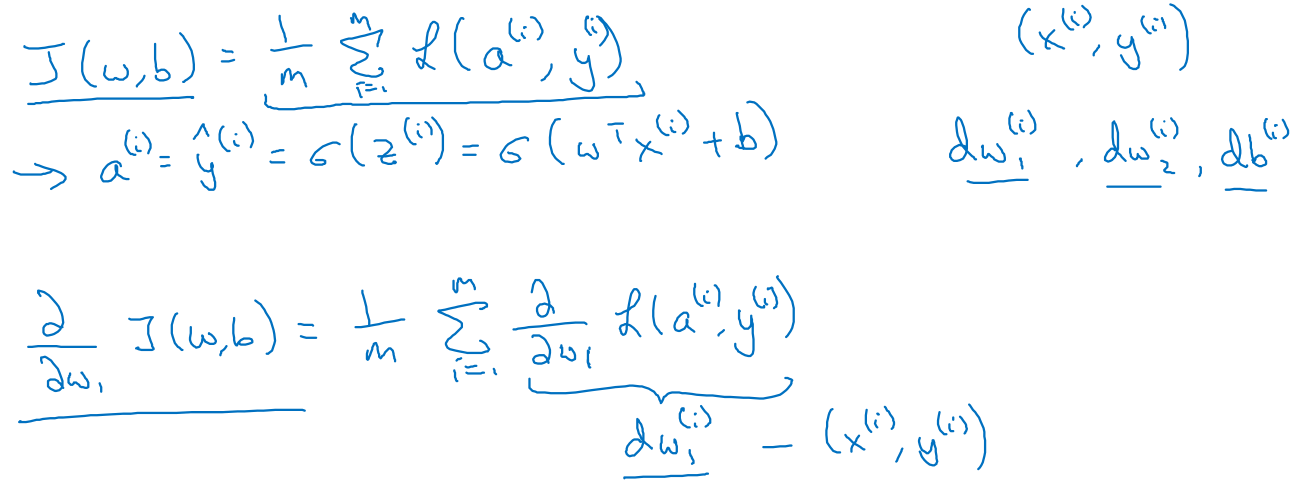
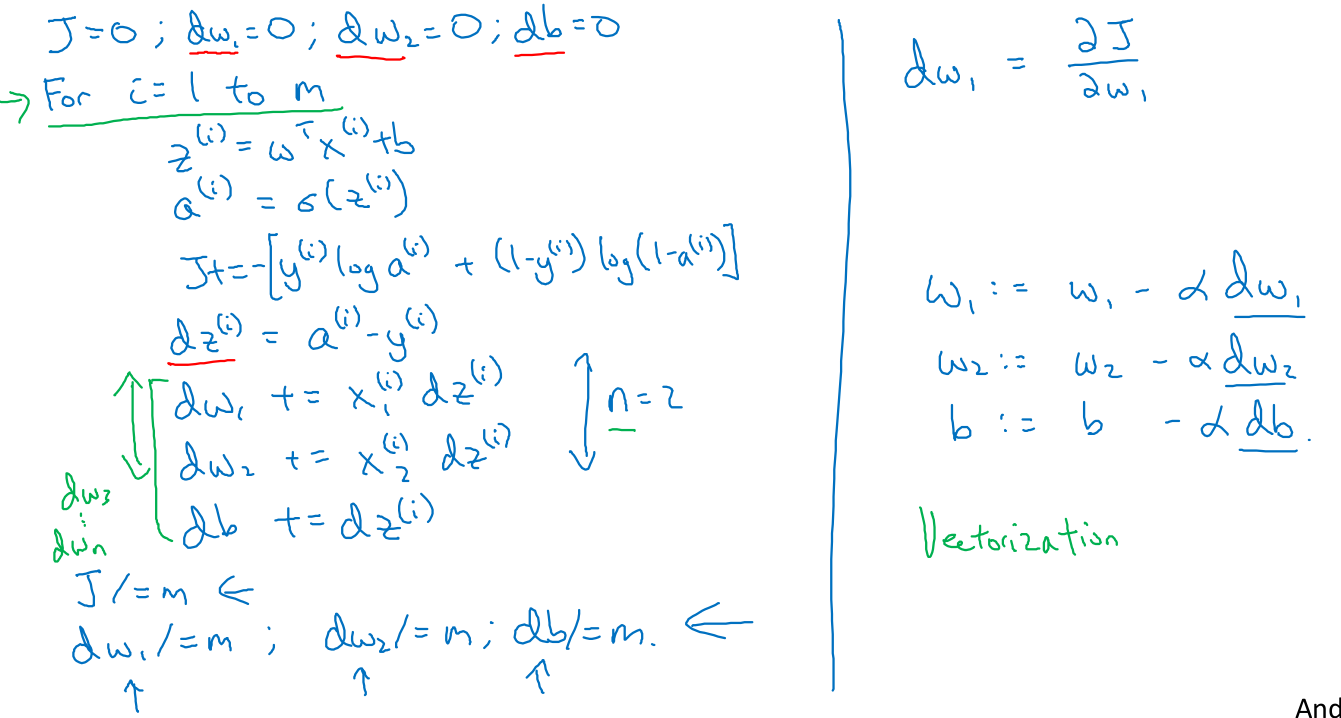
- m 개의 훈련세트에 대해 cost를 구하고 반대로 도함수를 구하면서 w, b를 구하고, 마지막에 평균으로 나눠 최적의 w, b를 찾는 코드를 확인할 수 있습니다.
- 이해안가는 부분이 몇개 있긴한데, 과제를 풀면서 해결하면 될 것 같습니다.
예상은 했지만 생각보다 만만하지 않은 과정이네요.
꽤나 열심히 해야되겠습니다.